Entering the Third Dimension
Colon definitions typically contain both control flow operators and stack flow
operators. In order to represent both these aspects of a program graphically we
need to move from two dimensional flowcharts to three dimensions. This is
illustrated here with two examples.
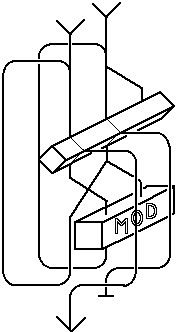
Euclid's Algorithm
In his seminal work "The Art of Computer Programming" D E Knuth devotes a
great deal of space to analyzing this algorithm. In volume 1, page 2 he describes
it thus;
Algorithm E. (Euclid's algorithm). given two positive integers
m and n , find their greatest common divisor, i.e., the largest
positive integer which evenly divides both m and n.
E1. [Find remainder.] Divide m by n and let r be
the remainder. (We will have 0<=r<n.)
E2. [Is it zero?] if r = 0, the algorithm terminates; n
is the answer.
E3. [Interchange.] Set m <- n, n <- r ,
and go back to step E1.
And here is the Forth code to do this; (the test for zero has been placed before
the division, so that it handles an argument of zero predictably).
: GCD ( n n--n) BEGIN DUP WHILE TUCK MOD REPEAT DROP ;
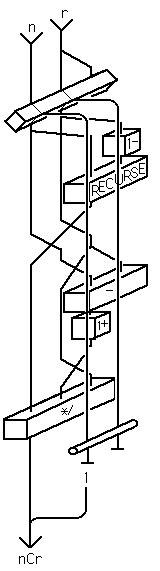
Combinations
There are many possible algorithms to find the number of combinations of r
items from n objects ( nCr). The two most commonly quoted are
n!/r!(n-r)!
and Vandermonde's theorem;
nCr = nC(r-1) + (n-1)Cr
The former has a problem in that very large intermediate results can occur, even
when the result is very small. The latter does not suffer from this, but is
computationally very inefficient.
Therefore we choose to use the following recurrance, which suffers from neither
of those setbacks;
r=0 --> nCr = 1
r>0 --> nCr = nC(r-1)(n-r+1)/r
This translates in Forth into;
: (COMBS) ( n r--c) DUP IF 2DUP 1- RECURSE
-ROT TUCK - 1+
SWAP */
ELSE 2DROP 1
THEN ;
Where the word RECURSE indicates that the definition is called
recursively.
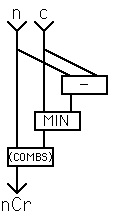 One refinement we can make to this is to note that the function is symmetrical,
i.e. that nCr = nC(n-r), so we can reduce the amount of work that the word may
do by choosing to compute the smaller of r and (n-r). To do this we can call
(COMBS)from another word that does the test. (Having interactively
tested (COMBS) first, naturally.)
One refinement we can make to this is to note that the function is symmetrical,
i.e. that nCr = nC(n-r), so we can reduce the amount of work that the word may
do by choosing to compute the smaller of r and (n-r). To do this we can call
(COMBS)from another word that does the test. (Having interactively
tested (COMBS) first, naturally.)
: COMBS ( n r--c) 2DUP - MIN (COMBS) ;
This concludes the body of this introduction to Forth. In the
last section we will mention some of the aspects of
Forth not covered here, and give some pointers to other information about Forth.
Or, if you prefer, you may return to the
contents page.
 One refinement we can make to this is to note that the function is symmetrical,
i.e. that nCr = nC(n-r), so we can reduce the amount of work that the word may
do by choosing to compute the smaller of r and (n-r). To do this we can call
(COMBS)from another word that does the test. (Having interactively
tested (COMBS) first, naturally.)
One refinement we can make to this is to note that the function is symmetrical,
i.e. that nCr = nC(n-r), so we can reduce the amount of work that the word may
do by choosing to compute the smaller of r and (n-r). To do this we can call
(COMBS)from another word that does the test. (Having interactively
tested (COMBS) first, naturally.)

